02.01.2020

Рідкісні невістки можуть похвалитися, що у них рівні і дружні відносини зі свекрухою. Зазвичай трапляється з точністю до навпаки

ПОХІДНА-проізводной функції y = f(x), Заданої на деякому інтервалі ( a, b) В точці xцього інтервалу, називається межа, до якого прагне відношення приросту функції fв цій точці до відповідного приросту аргументу, коли приріст аргументу прямує до нуля.

Похідну прийнято позначати так:

Широко вживаються і інші позначення:

Миттєва швидкість.

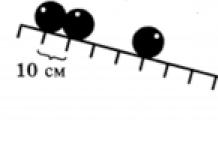
нехай точка Mрухається по прямій. відстань sрухається точки, що відраховується від деякого початкового її положення M 0 , Залежить від часу t, Тобто sє функція часу t: s= f(t). Нехай в деякий момент часу tрухається точка Mперебувала на відстані sвід початкового положення M 0, а в певний наступний момент t+ D tвиявилася в положенні M 1 - на відстані s+ D sвід початкового положення ( см. рис.).

Таким чином, за проміжок часу D tвідстань sзмінилося на величину D s. У цьому випадку говорять, що за проміжок часу D tвеличина sотримала приріст D s.

Середня швидкість не може у всіх випадках точно охарактеризувати швидкість переміщення точки Mв момент часу t. Якщо, наприклад, тіло на початку проміжку D tпереміщалася дуже швидко, а в кінці дуже повільно, то середня швидкість не зможе відобразити зазначених особливостей руху точки і дати уявлення про справжню швидкості її руху в момент t. Щоб точніше висловити щиру швидкість за допомогою середньої швидкості, треба взяти менший проміжок часу D t. Найбільш повно характеризує швидкість руху точки в момент tта межа, до якої прагне середня швидкість при D t® 0. Ця межа називають швидкістю руху в даний момент:

Таким чином, швидкістю руху в даний момент називається границя відношення приросту шляху D sдо збільшенню часу D t, Коли приріст часу прагне до нуля. Так як

Геометричне значення похідної. Дотична до графіка функції.

Побудова дотичних - одна з тих завдань, які привели до народження диференціального обчислення. Перший опублікований працю, що відноситься до диференціального числення і належить перу Лейбніца, мав назву Новий метод максимумів і мінімумів, а також дотичних, для якого не є перешкодою ні дробові, ні ірраціональні величини, і особливий для цього рід обчислення.

Нехай крива є графік функції y =f(x) В прямокутній системі координат ( см. Мал.).

При деякому значенні xфункція має значення y =f(x). цим значенням xі yна кривій відповідає точка M 0(x, y). якщо аргументу xдати приріст D x, То новому значенню аргументу x+ D xвідповідає нове значення функції y + D y = f(x + D x). Відповідною йому точкою кривої буде точка M 1(x+ D x,y+ D y). Якщо провести січну M 0M 1 і позначити через j кут, утворений січною з позитивним напрямком осі Ox, З малюнка безпосередньо видно, що.

Якщо тепер D xпрямує до нуля, то точка M 1 переміщається уздовж кривої, наближаючись до точки M 0, і кут j змінюється зі зміною D x. при Dx® 0 кут j прагне до деякого межі a і пряма, що проходить через точку M 0 і складова з позитивним напрямком осі абсцис кут a, буде шуканої дотичній. Її кутовий коефіцієнт:

отже, f´( x) = Tga

тобто значення похідної f´( x) При даному значенні аргументу xдорівнює тангенсу кута, утвореного дотичною до графіка функції f(x) У відповідній точці M 0(x,y) З позитивним напрямком осі Ox.

Диференційовність функцій.

Визначення. якщо функція y = f(x) Має похідну в точці x = x 0, то функція диференційована в цій точці.

Безперервність функції, що має похідну. Теорема.

якщо функція y = f(x) Диференційована в деякій точці x = x 0, то вона в цій точці неперервна.

Таким чином, в точках розриву функція не може мати похідної. Зворотне висновок невірно, тобто з того, що в якій-небудь крапці x = x 0 функція y = f(x) Неперервна не слід, що вона в цій точці дифференцируема. Наприклад, функція y = |x| неперервна для всіх x(-Ґ х x = 0 не має похідної. У цій точці не існує дотичної до графіка. Є права дотична і ліва, але вони не збігаються.

Деякі теореми про диференціюються функції. Теорема про коріння похідної (теорема Ролля).якщо функція f(x) Неперервна на відрізку [a,b], Диференційована у всіх внутрішніх точках цього відрізка і на кінцях x = aі x = bзвертається в нуль ( f(a) = f(b) = 0), то всередині відрізка [ a,b] Існує, принаймні одна, точка x= з, a c b, в якій похідна fў( x) Звертається в нуль, тобто fў( c) = 0.

Теорема про кінцевих збільшеннях (теорема Лагранжа).якщо функція f(x) Неперервна на відрізку [ a, b] І диференційована у всіх внутрішніх точках цього відрізка, то всередині відрізка [ a, b] Знайдеться принаймні одна точка з, a c b, що

f(b) – f(a) = fў( c)(b– a).

Теорема про ставлення збільшень двох функцій (теорема Коші).якщо f(x) і g(x) - дві функції, безперервні на відрізку [a, b] І диференціюються у всіх внутрішніх точках цього відрізка, причому gў( x) Ніде всередині цього відрізка не звертається до нуль, то всередині відрізка [ a, b] Знайдеться така точка x = з, a c b, що

Похідні різних порядків.

нехай функція y =f(x) дифференцируема на деякому відрізку [ a, b]. значення похідної f ў( x), Взагалі кажучи, залежать від x, Тобто похідна f ў( x) Являє собою теж функцію від x. При диференціюванні цієї функції виходить так звана друга похідна від функції f(x), Яка позначається f ўў ( x).

похідною n-го порядку від функції f(x) Називається похідна (першого порядку) від похідної n- 1- го і позначається символом y(n) = (y(n- 1)) ў.

Диференціали різних порядків.

диференціал функції y = f(x), Де x- незалежна змінна, є dy = f ў( x)dx, деяка функція від x, але від xможе залежати тільки перший співмножник f ў( x), Другий же співмножник ( dx) Є приростом незалежної змінної xі від значення цієї змінної не залежить. Так як dyє функція від x, То можна визначити диференціал цієї функції. Диференціал від диференціала функції називається другим диференціалом або диференціалом другого порядку цієї функції і позначається d 2y:

d(dx) = d 2y = f ўў( x)(dx) 2 .

диференціалом n-го порядку називається перший диференціал від диференціала n- 1- го порядку:

d n y = d(d n–1y) = f(n)(x)dx(n).

Приватна похідна.

Якщо функція залежить не від одного, а від декількох аргументів x i(iзмінюється від 1 до n,i= 1, 2,… n),f(x 1,x 2,… x n), То в диференціальному численні вводиться поняття похідної, яка характеризує швидкість зміни функції декількох змінних, коли змінюється тільки один аргумент, наприклад, x i. Приватна похідна 1-ого порядку по x iвизначається як звичайна похідна, при цьому передбачається, що всі аргументи, крім x i, Зберігають постійні значення. Для приватних похідних вводяться позначення

Певні таким чином приватні похідні 1-ого порядку (як функції тих же аргументів) можуть, в свою чергу, також мати приватні похідні, це приватні похідні другого порядку і т.д. Взяті з різних аргументів такі похідні називаються змішаними. Безперервні змішані похідні одного порядку не залежать від порядку диференціювання та є рівними між собою.

Анна Чугайнова

похідною функціїв точці називається границя відношення приросту функції до приросту аргументу, за умови, що прагне до нуля.

Основні правила знаходження похідної

Якщо - і - диференційовані функції в точці, (тобто функції, що мають похідні в точці), то:

Таблиця похідних основних функцій

1. 8.

2. 9.

3. 10.

5. 12.

6. 13.

7.

Правило диференціювання складної функції.Якщо і, тобто , Де і мають похідні, то

Диференціювання функції, заданої параметрично. Нехай залежність змінної від змінної задана параметрично за допомогою параметра:

завдання 3. Знайти похідні даних функцій.

1)

Рішення. Застосовуючи правило 2 знаходження похідних і формули 1 і 2 таблиці похідних, отримуємо:

Рішення.Застосовуючи правило 4 знаходження похідних і формули 1 і 13 таблиці похідних, отримуємо:

.

Рішення.Застосовуючи правило 3 знаходження похідних і формули 5 і 11 таблиці похідних, отримуємо:

Рішення.Вважаючи, де, згідно з формулою знаходження похідної складної функції, одержимо:

Рішення. Маємо: Тоді, відповідно до формули знаходження похідної функції, заданої параметрично, отримуємо:

4. Похідні вищих порядків. правило Лопіталя.

Похідною другого порядку функціїназивається похідна від її похідної, тобто . Для другої похідної використовуються наступні позначення: або, або.

Похідною - го порядку від функціїназивається похідна від її похідної -го порядку. Для похідною -го порядку можуть використовуватися такі символи: або, або.

Правило Лопіталя.Нехай функції і мають похідні в околиці точки, причому похідна не звертається до нуль. Якщо функції і є одночасно або нескінченно малими, або нескінченно великими при, і при цьому існує межа відносини при, то існує також і межа відносини при. причому

.

Правило може бути застосовано і в разі, коли.

Зауважимо, що в деяких випадках розкриття невизначеностей виду або може зажадати неодноразового застосування правила Лопіталя.

Невизначеності виду і т.д. за допомогою елементарних перетворень легко зводяться до невизначеностей виду або.

завдання 4. Знайти межа, користуючись правилом Лопіталя.

РішенняТут ми маємо невизначеність виду, тому що при. Застосуємо правило Лопіталя:

.

Після застосування правила Лопіталя ми знову отримали невизначеність виду, тому що при. Застосовуючи знову правило Лопіталя повторно, отримаємо:

.

5. Дослідження функцій

а) Зростання і спадання функцій

функція називається зростаючоїна відрізку , Якщо для будь-яких точок і з відрізка, де, має місце нерівність. Якщо функція неперервна на відрізку і при, то зростає на відрізку.

функція називається спадноїна відрізку , Якщо для будь-яких точок і з відрізка, де, має місце нерівність. Якщо функція неперервна на відрізку і при, то убуває на відрізку.

Якщо функція є тільки зростаючої або тільки спадної на даному інтервалі, то вона називається монотонноїна інтервалі.

b) Екстремуми функцій

точкою мінімумуфункції .

Якщо існує -окрестность точки така, що для всіх точок з цієї околиці має місце нерівність, то точка називається точкою максимумуфункції .

Точки максимуму і мінімуму функції називаються її точками екстремуму.

точка називається стаціонарної точкою,якщо або не існує.

Якщо існує -окрестность стаціонарної точки така, що при і при, то - точка максимуму функції.

Якщо існує -окрестность стаціонарної точки така, що при і при, то -точка мінімуму функції.

a) Напрямок опуклості. точки перегину

опуклим вгоруна інтервалі , якщовони розташований нижче дотичній, побудованої до графіка функції в будь-якій точці цього інтервалу.

Достатньою умовою опуклості вгору графіка функції на інтервалі є виконання нерівності для будь-якого з розглянутого інтервалу.

Графік функції, що диференціюється називається опуклим внизна інтервалі , якщовони розташований вище дотичній, побудованої до графіка функції в будь-якій точці цього інтервалу.

Достатньою умовою опуклості вниз графіка функції на інтервалі є виконання нерівності для будь-якого з розглянутого інтервалу.

Точка, в якій змінюється напрямок опуклості графіка функції, називається точкою перегину.

Точка, де або не існує, є абсцисою точки перегину, якщо зліва і праворуч від неї має різні знаки.

d) Асимптоти

Якщо відстань від точки графіка функції до деякої прямої прямує до нуля при нескінченному віддаленні точки від початку координат, то пряму називають асимптотой графіка функції.

Якщо існує число таке, що, то пряма є вертикальної асимптотой.

Якщо існують межі , То пряма є похилій (горизонтальної при k = 0) асимптотой.

e) Загальне дослідження функції

1. Область визначення функції

2. Точки перетину графіка з осями координат

3. Дослідження функції на неперервність, парність / непарність і періодичність

4. Інтервали монотонності функції

5. Точки екстремуму функції

6. Інтервали опуклості і точки перегину графіка функції

7. Асимптоти графіка функції

8. Графік функції.

завдання 5. Дослідити функцію і побудувати її графік.

Рішення. 1) Функція визначена на всій числовій осі за винятком точки, де знаменник дробу звертається в нуль. . Маємо: не належить області визначення даної функції. Отже, стаціонарними точками даної функції є точки, мінімальне значення (що показано на малюнку).

У завданні №7 профільного рівня ЄДІ з математики необхідно продемонструвати знання функції похідною і первісної. У більшості випадків достатньо просто визначення понять і розуміння значень похідної.

Розбір типових варіантів завдань №7 ЄДІ з математики профільного рівня

Перший варіант завдання (демонстраційний варіант 2018)

На малюнку зображений графік функції, що диференціюється y = f (x). На осі абсцис відзначені дев'ять точок: x 1, x 2, ..., x 9. Серед цих точок знайдіть всі крапки, в яких похідна функції y = f (x) негативна. У відповіді вкажіть кількість знайдених точок.

Алгоритм рішення:

1. Розглядаємо графік функції.
2. Шукаємо точки, в яких функція спадає.
3. Підраховуємо їх кількість.
4. Записуємо відповідь.

Рішення:

1. На графіку функція періодично зростає, періодично убуває.

2. У тих інтелвалах, де функція спадає, похідна має негативні значення.

3. У цих інтервалах лежать точки x 3 , x 4 , x 5 , x 9. Таких точок 4.

Другий варіант завдання (з Ященко, №4)

На малюнку зображений графік функції у = f (x). На осі абсцис відзначені точки -2, -1, 2, 4. В якій з цих точок значення похідної найбільше? У відповіді вкажіть цю точку.

Алгоритм рішення:

1. Розглядаємо графік функції.
2. Розглядаємо поведінку функції в кожній з точок і знак похідної в них.
3. Знаходимо точки в найбільшим значенням похідною.
4. Записуємо відповідь.

Рішення:

1. Функція має кілька проміжків убування і зростання.

2. Там, де функція спадає. Похідна має знак мінус. Такі точки є серед зазначених. Але на графіку є точки, в яких функція зростає. У них похідна позитивна. Це точки з абсциссами -2 і 2.

3. Розглянемо графік в точках з х = -2 і х = 2. У точці х = 2 функція крутіше йде вгору, значить дотична в цій точці має більший кутовий коефіцієнт. Отже, в точці з абсцисою 2. Похідна має найбільше значення.

Третій варіант завдання (з Ященко, №21)

Пряма є дотичною до графіка функції . Знайдіть а.

Алгоритм рішення:

1. Прирівняємо рівняння дотичній і функції.
2. Спрощуємо отримане рівність.
3. Знаходимо дискримінант.
4. визначаємо параметр а, При якому рішення єдине.
5. Записуємо відповідь.

Рішення:

1. Координати точки дотику задовольняють обом рівнянням: дотичній і функції. Тому ми можемо прирівняти рівняння. отримаємо:

2. Спрощуємо рівність, перенісши всі складові в одну сторону:

3. У точці дотику має бути одне рішення, тому дискриминант отриманого рівняння має дорівнювати нулю. Така умова єдиності кореня квадратного рівняння.

4. Отримуємо:

Якщо завдання вирішено правильно, то отримуєш 1 бал.

На рішення відводиться приблизно 5 хвилин.

Щоб вирішити завдання 7 по математиці профільного рівня необхідно знати:

1. Завдання поділяються на кілька видів:
   • фізичний зміст похідної.
   • геометричний зміст похідної і дотична;
   • застосування похідної до дослідження функцій;
   • Первісна.
2. Знання функції похідною і.
3. А в більшості випадків просто визначення понять і розуміння значень похідної.

• похідна - швидкість зміни функції. похідна позитивнана проміжках, на яких функція возрастаеті негативнана проміжках, на яких функц ия зменшується.
• Точки екстремуму, максимуму і мінімуму. точка екстремуму- максимальне / мінімальне значення функції на заданій множині. Якщо досягається найбільше значення, то точка екстремуму носить назву «точка максимуму», якщо досягається найменше значення, то точка екстремуму носить назву «точка мінімуму».
• Первісна. функцію F (x)називають первісною для функції f (х)на заданому проміжку, якщо для всіх хз цього проміжку виконується рівність F '(x) = f (x). Операція знаходження первісної функції називається інтегруванням.
• інтегрування - математичне дію, зворотне диференціювання, тобто знаходженню похідної. Інтегрування дозволяє по похідної функції знайти саму функцію.

Показує зв'язок знака похідної з характером монотонності функції.

Будь ласка, будьте гранично уважні в наступному. Дивіться, графік ЧОГО вам дано! Функції або її похідної

Якщо дан графік похідної, То цікавити нас будуть тільки знаки функції і нулі. Ніякі «горбки» і «западини» не цікавлять нас в принципі!

Завдання 1.

На малюнку зображено графік функції, визначеної на інтервалі. Визначте кількість цілих точок, в яких похідна функції негативна.

Рішення:

На малюнку виділені кольором області спадання функції:

У ці області спадання функції потрапляє 4 цілі значення.

Завдання 2.

На малюнку зображено графік функції, визначеної на інтервалі. Знайдіть кількість точок, в яких дотична до графіка функції паралельна прямій або збігається з нею.

Рішення:

Раз дотична до графіка функції паралельна (або збігається) прямий (або, що те ж саме,), має кутовий коефіцієнт, Рівний нулю, то і дотична має кутовий коефіцієнт.

Це в свою чергу означає, що дотична паралельна осі, так як кутовий коефіцієнт є тангенс кута нахилу дотичної до осі.

Тому ми знаходимо на графіку точки екстремуму (точки максимуму і мінімуму), - саме в них дотичні до графіка функції будуть паралельні осі.

Таких точок - 4.

Завдання 3.

На малюнку зображений графік похідної функції, визначеної на інтервалі. Знайдіть кількість точок, в яких дотична до графіка функції паралельна прямій або збігається з нею.

Рішення:

Раз дотична до графіка функції паралельна (або збігається) прямою, що має кутовий коефіцієнт, то і дотична має кутовий коефіцієнт.

Це в свою чергу означає, що в точках торкання.

Тому дивимося, скільки точок на графіку мають ординату, рівну.

Як бачимо, таких точок - чотири.

Завдання 4.

На малюнку зображено графік функції, визначеної на інтервалі. Знайдіть кількість точок, в яких похідна функції дорівнює 0.

Рішення:

Похідна дорівнює нулю в точках екстремуму. У нас їх 4:

Завдання 5.

На малюнку зображений графік функції і одинадцять точок на осі абсцис :. У скількох з цих точок похідна функції негативна?

Рішення:

На проміжках убування функції її похідна приймає негативні значення. А убуває функція в точках. Таких точок 4.

Завдання 6.

На малюнку зображено графік функції, визначеної на інтервалі. Знайдіть суму точок екстремуму функції.

Рішення:

точки екстремуму- це точки максимуму (-3, -1, 1) і точки мінімуму (-2, 0, 3).

Сума точок екстремуму: -3-1 + 1-2 + 0 + 3 = -2.

Завдання 7.

На малюнку зображений графік похідної функції, визначеної на інтервалі. Знайдіть проміжки зростання функції. У відповіді вкажіть суму цілих точок, що входять в ці проміжки.

Рішення:

На малюнку виділені проміжки, на яких похідна функції невід'ємна.

На малому проміжку зростання цілих точок немає, на проміжку зростання чотири цілих значення:,, і.

Їх сума:

Завдання 8.

На малюнку зображений графік похідної функції, визначеної на інтервалі. Знайдіть проміжки зростання функції. У відповіді вкажіть довжину найбільшого з них.

Рішення:

На малюнку виділені кольором все проміжки, на яких похідна позитивна, а значить сама функція зростає на цих проміжках.

Довжина найбільшого з них - 6.

Завдання 9.

На малюнку зображений графік похідної функції, визначеної на інтервалі. В якій точці відрізка приймає найбільше значення.

Рішення:

Дивимося як поводиться графік на відрізку, а саме нас цікавить тільки знак похідної .

Знак похідної на - мінус, так як графік на цьому відрізку нижче осі.

Про геометричний сенс написано багато теорії. Не буду вдаватися в висновок приросту функції, нагадаю основне для виконання завдань:

Похідна в точці x дорівнює кутовому коефіцієнту дотичної до графіка функції y = f (x) в цій точці, тобто це тангенс кута нахилу до осі Х.

Візьмемо відразу завдання з ЄДІ і почнемо в ньому розбиратися:

Завдання №1. На малюнку зображенографік функції y = f (x) і дотична до нього в точці з абсцисою x0. Знайдіть значення похідної функції f (x) в точці x0.
Хто дуже квапиться і не хоче розбиратися в поясненнях:будуйте до будь-якого такого трикутника (як показано нижче) і ділите стоячу сторону (вертикальну) на лежачу (горизонтальну) і буде вам щастя, якщо про символ не забудь (якщо пряма убуває (→ ↓), то відповідь має бути з мінусом, якщо пряма зростає (→), то відповідь має бути позитивний!)

Знайти потрібно кут між дотичній і віссю Х, назвемо його α: проведемо паралельну осі Х пряму в будь-якому місці через дотичну до графіка, отримаємо той же кут.

Краще не брати точку х0, тому що знадобиться велика лупа для визначення точних координат.

Взявши будь-який прямокутний трикутник (на малюнку запропоновано 3 варіанти), знайдемо tgα (кути, то рівні, як відповідні), тобто отримаємо похідну функції f (x) в точці x0. Чому ж так?

Якщо ми проведемо дотичні в інших точках x2, x1 і т.д. дотичні будуть інші.

Повернемося до 7 класу, щоб побудувати пряму!

Рівняння прямої задається рівнянням y = kx + b, де

k - нахил щодо осі Х.

b - відстань між точкою перетину з віссю Y і початком координат.

Похідна прямий, завжди одна і та ж: y "= k.

В якій би точці на прямій ми не взяли похідну, вона буде незмінна.

Тому, залишилося тільки знайти tgα (як було сказано вище: ділимо стоячу сторону на лежачу). Ділимо протилежний катет на прилеглий, отримуємо, що k = 0,5. Однак, якщо графік убуває, коефіцієнт негативний: k = -0,5.

Раджу себе перевіряти другим способом:
По двох точках можна задати пряму. Знайдемо координати двох будь-яких точок. Наприклад, (-2; -2) і (2; -4):

Підставами в рівняння y = kx + b замість y і х координати точок:

-2 = -2k + b

Вирішивши цю систему, отримаємо b = -3, k = -0,5

Висновок: Другий спосіб довше, але в ньому ви не забудете про знак.

Відповідь: - 0,5

Завдання №2. На малюнку зображений графік похідноїфункції f (x). На осі абсцис відзначені вісім точок: x1, x2, x3, ..., x8. Скільки з цих точок лежить на проміжках зростання функції f (x)?

Якщо графік функції убуває - похідна негативна (вірно і навпаки).

Якщо графік функції зростає - похідна позитивна (вірно і навпаки).

Ці дві фрази допоможуть вам вирішити більшу частину завдань.

Уважно дивіться, малюнок похідною вам дано або функції, а далі вибирайте одну з двох фраз.

Побудуємо схематично графік функції. Оскільки нам дано графік похідної, то там, де вона негативна, графік функції убуває, де позитивна - зростає!

Виходить, що 3 точки лежать на ділянках зростання: x4; x5; x6.

Відповідь: 3

Завдання №3. Функція f (x) визначена на проміжку (-6; 4). На малюнку зображений графік її похідної. Знайдіть абсциссу точки, в якій функція приймає найбільше значення.

Раджу завжди будувати, як йде графік функції, такими стрілочками або схематично зі знаками (як в №4 та №5):

Очевидно, якщо графік зростає до -2, то максимальна точка і є -2.

Відповідь: -2

Завдання №4. На малюнку зображений графік функції f (x) і дванадцять точок на осі абсцис: x1, x2, ..., x12. У скількох з цих точок похідна функції негативна?

Завдання зворотна, дан графік функції, потрібно схематично побудувати, як буде виглядати графік похідної функції, і порахувати, скільки точок буде лежати в негативному діапазоні.

Позитивні: x1, x6, x7, x12.

Негативні: x2, x3, x4, x5, x9, x10, x11.

Відповідь: 7

Ще один вид завдань, коли питається про якісь страшні "екстремуми"? Що це таке вам знайти не важко, я ж поясню для графіків.

Завдання №5. На малюнку зображений графік похідної функції f (x), визначеної на інтервалі (-16; 6). Знайдіть кількість точок екстремуму функції f (x) на відрізку [-11; 5].

Відзначимо проміжок від -11 до 5!

Звернемо свої ясні очі на табличку: дан графік похідної функції => тоді екстремуми це точки перетину з віссю X.

Відповідь: 3

Завдання №6. На малюнку зображений графік похідної функції f (x), визначеної на інтервалі (-13; 9). Знайдіть кількість точок максимуму функції f (x) на відрізку [12; 5].

Відзначимо проміжок від -12 до 5!

Можна одним оком поглянути в табличку, точка максимуму - це екстремум, такий, що до нього похідна позитивна (функція зростає), а після нього похідна негативна (функція спадає). Такі точки обведені в кружечок.

Стрілочками показано, як веде себе графік функції

Відповідь: 3

Завдання №7. На малюнку зображено графік функції f (x), визначеної на інтервалі (-7; 5). Знайдіть кількість точок, в яких похідна функції f (x) дорівнює 0.

Можна подивитися на вище наведену табличку (похідна дорівнює нулю, значить це точки екстремуму). А в даній задачі дано графік функції, значить потрібно знайти кількість точок перегину!

А можна, як зазвичай: будуємо схематичний графік похідної.

Похідна дорівнює нулю, коли графік функцій змінює свій напрямок (з зростання на спадання і навпаки)

Відповідь: 8

Завдання №8. На малюнку зображений графік похідноїфункції f (x), визначеної на інтервалі (-2; 10). Знайдіть проміжки зростання функції f (x). У відповіді вкажіть суму цілих точок, що входять в ці проміжки.

Побудуємо схематично графік функції:

Там, де він зростає, отримуємо 4 цілі точки: 4 + 5 + 6 + 7 = 22.

Відповідь: 22

Завдання №9. На малюнку зображений графік похідноїфункції f (x), визначеної на інтервалі (-6; 6). Знайдіть кількість точок f (x), в яких дотична до графіка функції паралельна прямій y = 2x + 13 або збігається з нею.

Нам дано графік похідної! Значить, і нашу дотичну потрібно «перевести» в похідну.

Похідна дотичній: y "= 2.

А тепер побудуємо обидві похідні:

Дотичні перетинаються в трьох точках, значить, наша відповідь 3.

Відповідь: 3

Завдання №10. На малюнку зображено графік функції f (x), і відзначені точки -2, 1, 2, 3. У якій з цих точок значення похідної найменше? У відповіді вкажіть цю точку.

Завдання чимось схоже на перше: щоб знайти значення похідної, потрібно побудувати дотичну до цього графіку в точці і знайти коефіцієнт k.

Якщо пряма убуває, k< 0.

Якщо пряма зростає, k> 0.

Подумаємо, як значення коефіцієнта відіб'ється на нахилі прямої:

При k = 1 або k = - 1 графік буде посередині між осями Х і У.

Чим ближче пряма до осі Х, тим ближче коефіцієнт k нулю.

Чим ближче пряма до осі Y, тим ближче коефіцієнт k до нескінченності.

У точці -2 і 1 k<0, однако в точке 1 прямая убывает "быстрее" больше похоже на ось Y =>саме там і буде найменше значення похідної

Відповідь: 1

Завдання №11. Пряма є дотичною y = 3x + 9 до графіка функції y = x³ + x² + 2x + 8. Знайдіть абсциссу точки дотику.

Пряма буде дотичної до графіка, коли графіки мають спільну точку, як і їх похідні. Прирівняємо рівняння графіків і їх похідні:

Вирішивши друге рівняння, отримуємо 2 точки. Щоб перевірити, яка з них підходить, підставляємо в перше рівняння кожен з іксів. Підійде тільки один.

Кубічне рівняння зовсім вирішувати не хочеться, а квадратне за милу душу.

Ось тільки, що записувати у відповідь, якщо вийде два "нормальних" відповіді?

При підстановці ікси (х) в початкові графіки y = 3x + 9 і y = x³ + x² + 2x + 8 повинен вийти один і той же Y

y = 1³ + 1² + 2 × 1 + 8 = 12

Вірно! Значить x = 1 і буде відповіддю

Відповідь: 1

Завдання №12. Пряма y = - 5x - 6 є дотичною до графіка функції ax² + 5x - 5. Знайдіть a.

Аналогічно прирівняємо функції і їх проівзодние:

Вирішимо цю систему щодо змінних a і x:

Відповідь: 25

Завдання з похідними вважається одним з найскладніших в першій частині ЄДІ, однак, при невеликої частки уважності і розуміння питання у вас все вийде, і ви піднімете відсоток виконання цього завдання!